In rencent days, I researched a mesh simplification algorithm
I will not talk about the details of this algorithm here. In short, the algorithm describes the cost of mesh edge contraction using quadric error metrics. After this mathematical modeling, we can use algebra theory to calc the extreme value of errors. That is the best contraction position on geometry side.
So, it is an interesting project which combines algebra and geometry. Following is my rough implementation.
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
public class VertexData
{
public Matrix4x4 errorMatrix = Matrix4x4.zero;
public List<int> edges = new List<int>();
public List<float> errors = new List<float>();
public List<Vector3> vBest = new List<Vector3>();
public void Combine(VertexData d)
{
errorMatrix = MathUtil.AddMatrix(errorMatrix, d.errorMatrix);
edges.AddRange(d.edges);
edges = edges.Distinct().ToList();
}
public void RemoveEdge(int vIndex)
{
int edgeIndex = edges.IndexOf(vIndex);
if (edgeIndex >= 0)
{
edges.RemoveAt(edgeIndex);
errors.RemoveAt(edgeIndex);
vBest.RemoveAt(edgeIndex);
}
for (int i = 0; i < edges.Count; i++)
{
if (edges[i] > vIndex)
edges[i] -= 1;
}
}
}
public class MathUtil
{
public static Matrix4x4 AddMatrix(Matrix4x4 m0, Matrix4x4 m1)
{
Matrix4x4 ret = new Matrix4x4();
for (int i = 0; i < 4; i++)
{
ret.SetRow(i, m0.GetRow(i) + m1.GetRow(i));
}
return ret;
}
}
public class QuadricErrorMetrics : MonoBehaviour
{
[SerializeField] Mesh input;
MeshFilter meshFilter;
List<Vector3> vertices;
List<int> triangles;
List<VertexData> vertexDatas = new List<VertexData>();
private void Start()
{
Init();
}
private void Init()
{
meshFilter = GetComponent<MeshFilter>();
vertices = new List<Vector3>(input.vertices);
triangles = new List<int>(input.triangles);
InitVertexData();
UpdateMesh();
InvokeRepeating("ContractCoroutine", 0 , 0.001f);
}
void InitVertexData()
{
for (int i = 0; i < vertices.Count; i++)
{
VertexData data = new VertexData();
data.edges = GetEdges(i);
vertexDatas.Add(data);
}
//int error metrics
for (int i = 0; i < triangles.Count; i += 3)
{
int v0 = triangles[i];
int v1 = triangles[i + 1];
int v2 = triangles[i + 2];
Vector3 p0 = vertices[v0];
Vector3 p1 = vertices[v1];
Vector3 p2 = vertices[v2];
Vector3 normal = Vector3.Cross(p1 - p0, p2 - p1).normalized;
float a = normal.x;
float b = normal.y;
float c = normal.z;
float d = -Vector3.Dot(normal, p0);
Matrix4x4 q = new Matrix4x4();
q.SetRow(0, new Vector4(a * a, a * b, a * c, a * d));
q.SetRow(1, new Vector4(b * a, b * b, b * c, b * d));
q.SetRow(2, new Vector4(c * a, c * b, c * c, c * d));
q.SetRow(3, new Vector4(d * a, d * b, d * c, d * d));
vertexDatas[v0].errorMatrix = MathUtil.AddMatrix(vertexDatas[v0].errorMatrix, q);
vertexDatas[v1].errorMatrix = MathUtil.AddMatrix(vertexDatas[v1].errorMatrix, q);
vertexDatas[v2].errorMatrix = MathUtil.AddMatrix(vertexDatas[v2].errorMatrix, q);
}
//Init Errors
for (int i = 0; i < vertexDatas.Count; i++)
{
CalcError(i);
}
}
void CalcError(int i)
{
var vertexData = vertexDatas[i];
vertexData.errors.Clear();
vertexData.vBest.Clear();
for (int j = 0; j < vertexData.edges.Count; j++)
{
int edge0 = i;
int edge1 = vertexData.edges[j];
if (Mathf.Approximately(Vector3.Distance(vertices[edge0], vertices[edge1]), 0))
{
vertexData.errors.Add(-1);
vertexData.vBest.Add(vertices[edge0]);
continue;
}
Matrix4x4 errorCombine = MathUtil.AddMatrix(vertexDatas[edge0].errorMatrix, vertexDatas[edge1].errorMatrix);
Matrix4x4 differentialMatrix = new Matrix4x4();
differentialMatrix.SetRow(0, new Vector4(errorCombine.m00, errorCombine.m01, errorCombine.m02, errorCombine.m03));
differentialMatrix.SetRow(1, new Vector4(errorCombine.m01, errorCombine.m11, errorCombine.m12, errorCombine.m13));
differentialMatrix.SetRow(2, new Vector4(errorCombine.m02, errorCombine.m12, errorCombine.m22, errorCombine.m23));
differentialMatrix.SetRow(3, new Vector4(0, 0, 0, 1));
Vector4 vbest = differentialMatrix.inverse * new Vector4(0, 0, 0, 1);
float error = Vector4.Dot(vbest, errorCombine * vbest);
if (differentialMatrix.determinant == 0)
{
Vector3 p0 = vertices[edge0];
Vector3 p1 = vertices[edge1];
Vector3 mid = (p0 + p1) / 2;
float errorP0 = Vector4.Dot(p0, errorCombine * p0);
float errorP1 = Vector4.Dot(p1, errorCombine * p1);
float errorMid = Vector4.Dot(mid, errorCombine * mid);
if (errorP0 <= errorP1 && errorP0 <= errorMid)
{
vbest = p0;
error = errorP0;
}
else if (errorP1 <= errorP0 && errorP1 <= errorMid)
{
vbest = p1;
error = errorP1;
}
else
{
vbest = mid;
error = errorMid;
}
}
//bounding box
if (Mathf.Abs(vbest.x) > 0.2f || Mathf.Abs(vbest.y) > 0.2f || Mathf.Abs(vbest.z) > 0.2f)
{
vertexData.errors.Add(float.MaxValue);
vertexData.vBest.Add(Vector3.zero);
continue;
}
if (error < 0)
error = 0;
vertexData.errors.Add(error);
vertexData.vBest.Add(vbest);
}
}
List<int> GetEdges(int v)
{
List<int> ret = new List<int>();
//add real edge
for (int i = 0; i < triangles.Count; i += 3)
{
for (int j = 0; j < 3; j++)
{
int index = i + j;
if (triangles[index] == v)
{
ret.Add(triangles[i]);
ret.Add(triangles[i + 1]);
ret.Add(triangles[i + 2]);
}
}
}
//close vertices can be a edge
Vector3 pos = vertices[v];
for (int i = 0; i < vertices.Count; i++)
{
if (Vector3.Distance(vertices[i], pos) < 0.01f)
{
ret.Add(i);
}
}
ret.RemoveAll(vertex => vertex == v);
return ret.Distinct().ToList();
}
void FindBestContract(out int v0, out int v1, out Vector3 newPos)
{
float minError = float.MaxValue;
VertexData target = null;
int targetIndex = 0;
foreach (var vd in vertexDatas)
{
float min = float.MaxValue;
foreach (var e in vd.errors)
{
if (e < min)
{
min = e;
}
}
if (min <= minError)
{
minError = min;
target = vd;
targetIndex = vd.errors.IndexOf(min);
}
}
v0 = vertexDatas.IndexOf(target);
v1 = target.edges[targetIndex];
newPos = target.vBest[targetIndex];
}
void ContractCoroutine()
{
if (vertices.Count > 50)
{
int v0, v1;
Vector3 newPos;
FindBestContract(out v0, out v1, out newPos);
Contract(v0, v1, newPos);
UpdateMesh();
}
}
void Contract(int v0, int v1, Vector3 newPos)
{
//merge v0 and v1 into end of vertexDatas
int newVertexId = vertices.Count;
vertices.Add(newPos);
VertexData newVertexData = new VertexData();
newVertexData.Combine(vertexDatas[v0]);
newVertexData.Combine(vertexDatas[v1]);
vertexDatas.Add(newVertexData);
CalcError(newVertexId);
if (v0 < v1)
{
int vt = v0;
v0 = v1;
v1 = vt;
}
vertices.RemoveAt(v0);
vertexDatas.RemoveAt(v0);
vertices.RemoveAt(v1);
vertexDatas.RemoveAt(v1);
foreach (var vertexData in vertexDatas)
{
vertexData.RemoveEdge(v0);
vertexData.RemoveEdge(v1);
}
//create edge from newVertexData (a, b) to (b, a)
int finalId = vertexDatas.Count - 1;
for (int i = 0; i < newVertexData.edges.Count; i++)
{
int v = newVertexData.edges[i];
vertexDatas[v].edges.Add(finalId);
vertexDatas[v].errors.Add(newVertexData.errors[i]);
vertexDatas[v].vBest.Add(newVertexData.vBest[i]);
}
// update triangles vertex id
for (int i = triangles.Count - 1; i >= 2; i -= 3)
{
int hitCount = 0;
for (int j = 0; j < 3; j++)
{
int index = i - j;
int vertex = triangles[index];
bool hit = false;
if (vertex == v0 || vertex == v1)
{
hit = true;
hitCount++;
}
if (hit)
{
if (hitCount == 1)
{
triangles[index] = newVertexId;
}
else if (hitCount == 2)
{
triangles.RemoveAt(i);
triangles.RemoveAt(i - 1);
triangles.RemoveAt(i - 2);
break;
}
}
}
}
for (int i = 0; i < triangles.Count; i++)
{
int vertex = triangles[i];
int sub = 0;
if (vertex > v0)
sub += 1;
if (vertex > v1)
sub += 1;
triangles[i] = vertex - sub;
}
}
void UpdateMesh()
{
Mesh output = new Mesh();
output.vertices = vertices.ToArray();
output.triangles = triangles.ToArray();
output.RecalculateNormals();
meshFilter.mesh = output;
}
}
Here is my test result with Stanford Bunny
- 3876 vertices
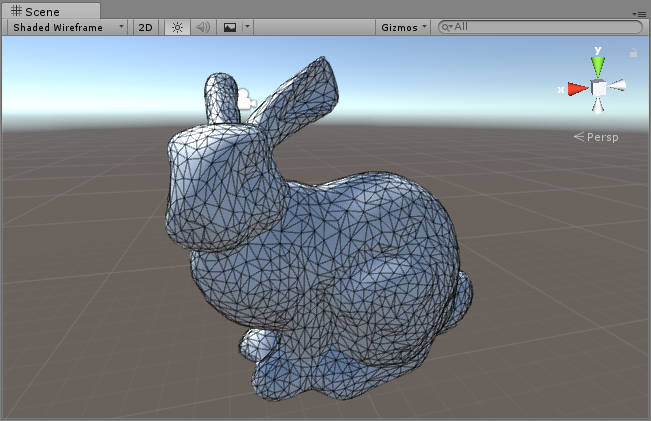
- 1147 vertices
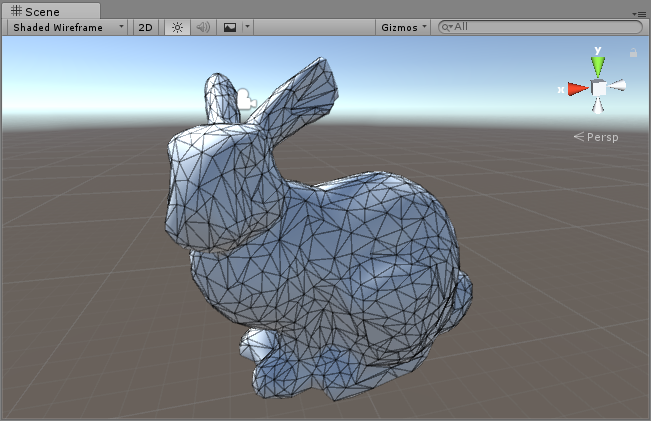
- 273 vertices
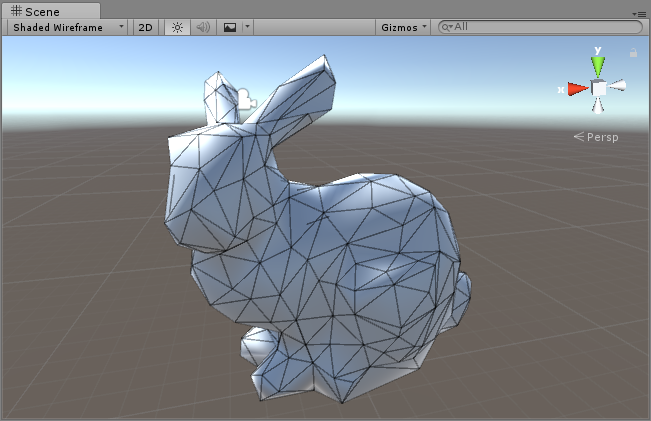
- 50 vertices
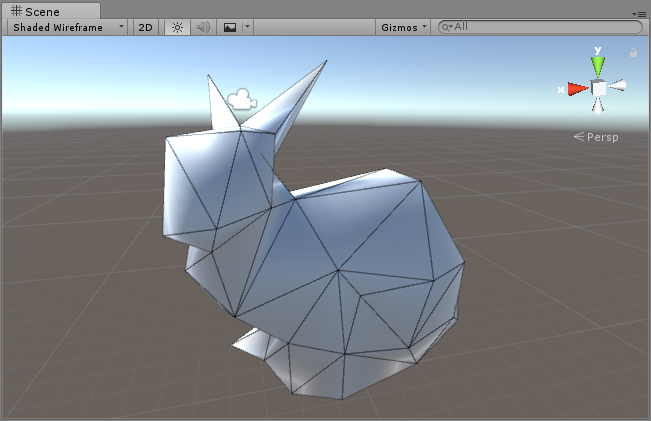
The result is cool!