In this part, I will talk about the details in my unity SmallPt based on David Cline’s ppt.
The Algorithm
Steps
- For each fragment, send a camera-to-screenpoint ray.
- This ray hits the first object, accumulate the color in the hit point.
- Diffuse, Reflect or refract in the hit point, generate a new diffuse, refelct or refract ray.
- Do step two and three again, until loop time is beyond MAXDEPTH or cannot hit any object.
- Since there are some randomness in each traced ray, we need to send several ray samples in a single fragment and calc their average color.
Russian Roulette
In Kevin Beason’s origin implementation, he used Russian Roulette algorithm. Russian Roulette randomly terminates a path with a probability, which increases when the trace depth grows.
This will reduce unnecessary traces and save compute resources. Besides, it boosts the energy of the non-terminated paths by their probability to be terminated. That keeps the algorithm unbiased.
Diffuse
Monte Carlo Method
Since diffuse has random direction, it’s hard to simulate data in all directions. So we can use Monte Carlo method to generate diffuse ray in random directions in a hemisphere.
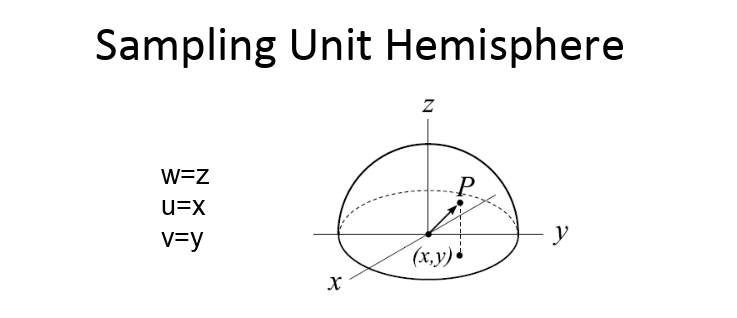
float3 jitter(float3 d, float phi, float sina, float cosa) {
float3 w = normalize(d), u = normalize(cross(w.yzx, w)), v = cross(w, u);
return (u*cos(phi) + v*sin(phi)) * sina + w * cosa;
}
float r2 = rand();
float3 d = jitter(nl, 2.*PI*rand(), sqrt(r2), sqrt(1. - r2));
Explicit Lighting And Implicit Lighting
Explicit Lighting: when a ray hits an object, check whether the hit point can be seen by the light source, calc the color created by the light source
Implicit Lighting: only calc the color created in the tracing path
Use explicit lighting can increase the total speed of rendering a full picture.
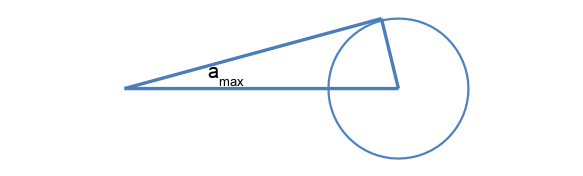
float cos_a_max = sqrt(1. - clamp(s.r * s.r / dot(l0, l0), 0., 1.));
float cosa = lerp(cos_a_max, 1., rand());
float3 l = jitter(l0, 2.*PI*rand(), sqrt(1. - cosa*cosa), cosa);
Ray rTemp = {x, l};
if (intersect(rTemp, t, s, id) == i) {
float omega = 2. * PI * (1. - cos_a_max);
e += (s.e * clamp(dot(l, n),0.,1.) * omega) / PI;
}
float omega = 2. * PI * (1. - cos_a_max);
It’s the solid angle of luminance area
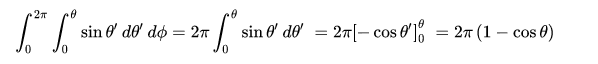
e += (s.e * clamp(dot(l, n),0.,1.) * omega) / PI;
- s.e is Radiance of lighting source.
- Multiply solid angle, we can get the input Irradiance in hit point.
- Since output Irradiance spreads in a hemisphere, so we should divide PI to input Irradiance. And here is the detail calculation. Cd is coefficient of diffuse BRDF.
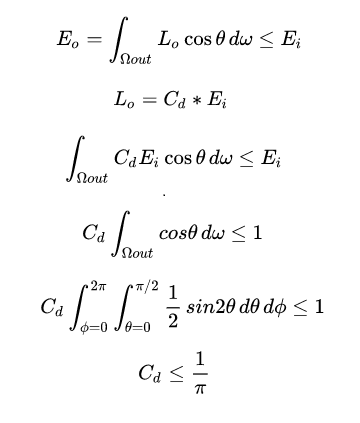
Reflection
This is much simpler than diffuse. We only need to calc new reflection ray direction by normal.
reflect(r.d, n)Refraction
Refraction Direction
We can calc refraction direction by object IOC.
float a=dot(n,r.d), ddn=abs(a); float nc=1., nt=1.5, nnt=lerp(nc/nt, nt/nc, float(a>0.)); float cos2t=1.-nnt*nnt*(1.-ddn*ddn); Ray rTemp = {x, reflect(r.d, n)}; r = rTemp; if (cos2t>0.) { float3 tdir = normalize(r.d*nnt + sign(a)*n*(ddn*nnt+sqrt(cos2t))); }Refration Amount
Some lighting energy is reflected on the surface, which is called Fresnel Reflectance.
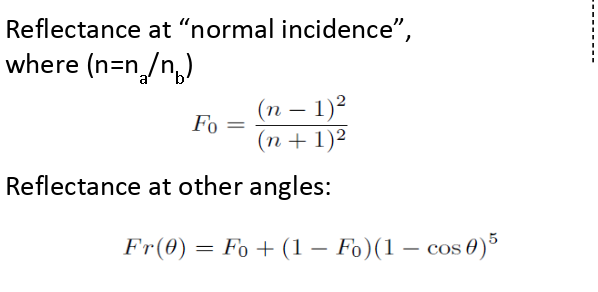We can use this equation to calculate reflection and refraction energy amount to create a more realistic refraction.float R0=(nt-nc)*(nt-nc)/((nt+nc)*(nt+nc)),c = 1.-lerp(ddn,dot(tdir, n),float(a>0.)); float Re=R0+(1.-R0)*c*c*c*c*c,P=.25+.5*Re,RP=Re/P,TP=(1.-Re)/(1.-P); if (rand()<P) { mask *= RP; } else { mask *= obj.c*TP; Ray rTemp = {x, tdir}; r = rTemp; }Conclusion
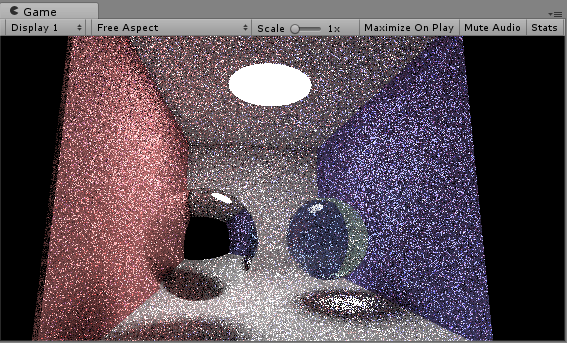In this practice of ray tracing, I learned the basic algoirithm of path tracing. Also, I met some new relevant knowledges and see the final view result. Still, I want to learn more and practice more.
