Volume Rendering Practice In Unity(Part One)

In traditional rendering pipeline, we just post preset vertices to gpu and get what shape we want. However, these triangles seem to be sharp and cold. When we want to draw a sphere, we need to create enough triangles to hide their sharp. Luckily, we have volume rendering. So today I will try raymarching to render some simple shapes in Unity.

Raymarching algorithm

• render a simple mesh which can restrict rendering area
• in fragment shading, draw a ray to view direction. Step by step, check whether the ray hits our target shape. If hits, shade with target shape color.
• lighting related shading to make this shape vivid

Practice in Unity

According to algorithm steps, I try to render a sphere. Render a cube mesh

That is easy. Create a cube(2 * 2 * 2). In fragment shader, return a fixed color.

fixed4 frag(v2f i) : SV_Target  
{   
    return fixed4(1,1,1,1);
}

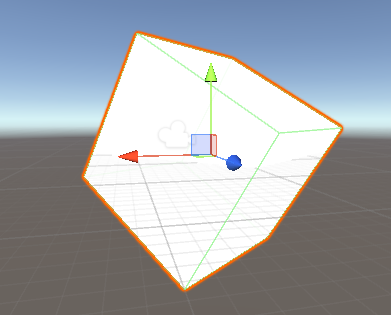Raymarching

First, we need a function to test the distance between target point and sphere center.

float Distance(float3 p, float3 center, float r)
{
    return distance(p,center) - r;
}

Then, we can create the core RayMarching function. In the for loop, we check the distance between point and sphere. If distance is below zero, the ray can hit the sphere, set return color to shpere color.

#define MAX_STEP 256
#define STEP 0.01
fixed4 RayMarching(float3 position, float3 direction)
{
    for(int i = 0; i < MAX_STEP; i++)
    {
        float distance = Distance(position, float3(0,0,0), 1);
        if(distance < 0)
            return fixed4(1,0.64705,0,1);
        position += STEP * direction;
    }
    return fixed4(1,1,1,1);
}

Finally, call RayMarching in fragment shader.

fixed4 frag(v2f i) : SV_Target  
{   
    float3 worldPos = i.worldPos;
    float3 direction = normalize(i.worldPos - _WorldSpaceCameraPos);
    return RayMarching(worldPos, direction);
}

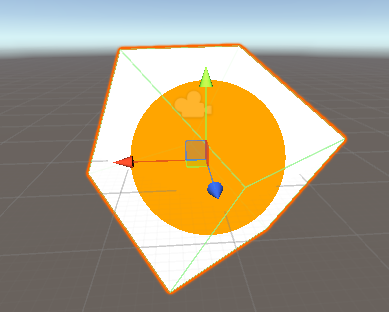Yeah, we create a sphere in a cube! It’s totally mathmatical! We can set alpha to 0 in raymarching failed area. Then we can get just a sphere. 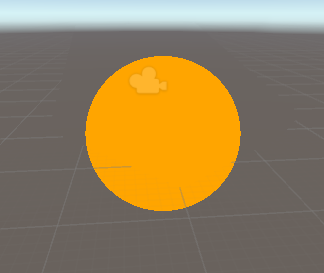Lighting

Now, the sphere seems to be a 2D sphere. We need to add some lighting to it. We can add following lighting function

fixed4 simpleLight (fixed4 color, fixed3 normal, float3 viewDirection) 
{
    fixed3 lightDir = _WorldSpaceLightPos0.xyz;
    fixed3 lightCol = _LightColor0.rgb;
    //Lambert
    fixed NdotL = max(dot(normal, lightDir),0);
    //Specular
    fixed3 h = (lightDir - viewDirection) / 2;
    fixed s = pow( dot(normal, h), _SpecularPower) * _Gloss;

    fixed4 c;
    c.rgb = color * lightCol * NdotL + s;
    c.a = 1;
    return c;
}

To calc lighting, we need to calc normal value of the virtual sphere.

float map(float3 p)
{
    return Distance(p, float3(0,0,0), 1));
}
float3 normal (float3 p)
{
    const float eps = 0.01;

    return normalize
    (	float3
        (	
            map(p + float3(eps, 0, 0)	) - map(p - float3(eps, 0, 0)),
            map(p + float3(0, eps, 0)	) - map(p - float3(0, eps, 0)),
            map(p + float3(0, 0, eps)	) - map(p - float3(0, 0, eps))
        )
    );
}

Distance Field

To now, we create a volume sphere. Function Distance is a mathmatical statement for shape sphere. We can change this function to draw different shape. Further more, we can blend two Distance function to get some interesting animation.

Conclusion

It’s an interesting experiment about rendering. My practice is based on Alan Zucconi’s blog. I hope I can have more opportunities to explore more hidden mathmatical bueaty in rendering.

• Next
  Volume Rendering Practice In Unity(Part Two)